数据结构中的树

今天刚好有机会复习了下数据结构里的树，悲哀的发现基本快忘光啦！看来是需要做点记录什么的了！
正好前几天学 JDBC 的时候在数据库设计的时候还有点这方面的东西没说，这次一并补上！

二叉树性质

非空二叉树的第 n 层上至多有 2^(n-1) 个元素。
深度为 h 的二叉树至多有 2^h-1 个结点。

满二叉树

在满二叉树中若其深度为h，则其所包含的结点数必为 2^h-1 。
所有终端都在同一层次，且非终端结点的度数为2。
通俗讲就是： 要么是叶子结点(结点的度为0)，要么结点同时具有左右子树 (结点的度为 2 )。

完全二叉树

完全二叉树是由满二叉树而引出来的。对于深度为 K 的，有 n 个结点的二叉树，当且仅当其每一个结点都与深度为 K 的满二叉树中编号从 1 至 n 的结点一一对应时称之为完全二叉树。
就是说：每层结点都完全填满，在最后一层上如果不是满的，则只缺少右边的若干结点，就是不能出现只有右边没有左边的情况，你可以都没有或者只有左边，或者都有。
对于完全二叉树，设一个结点为 i 则其父节点为 i/2 ，2i 为左子节点，2i+1 为右子节点。

二叉树的遍历

主要说的是深度优先的遍历方法，使用的均是递归的思想

先序遍历
根-左-右
中序遍历
左-根-右
后序遍历
左-右-根

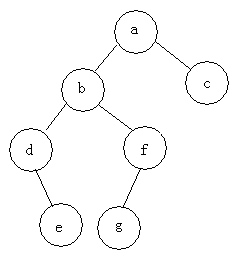
前序遍历：abdefgc
中序遍历：debgfac
后序遍历：edgfbca
层次遍历(广度优先了)：abcdfeg

根据序列画二叉树

这应该是考试最喜欢的题目了，给两个遍历序列让你还原二叉树啥的
要还原出二叉树，必须要给一个 中序遍历 的序列才行，另外一个无所谓了

套路就是根据先序遍历或者后序遍历确定根的位置，然后根据中序遍历确定左右分支
来个栗子：
已知：先序遍历为： abdgcefh ；中序遍历为：dgbaechf；方便起见，先序遍历编号为1号，另一个为2号

下面开始画，首先根据先序遍历确定根是 a；然后再看2号，dgb |a| echf ；这样就分开了，左边的是左半枝，右边的是右半枝；先画左半枝吧，那要先确定左边的根是谁，也就是 a 的孩子是谁，拿着左半边的 dgb 去1号找，发现 b 在最前面，先序遍历最前面的就是根啦！所以就确定 a 的左孩子就是 b 了，然后再用 b 根据2号确定左半枝是 dg，右半枝是空，然后依次类推…最后得出：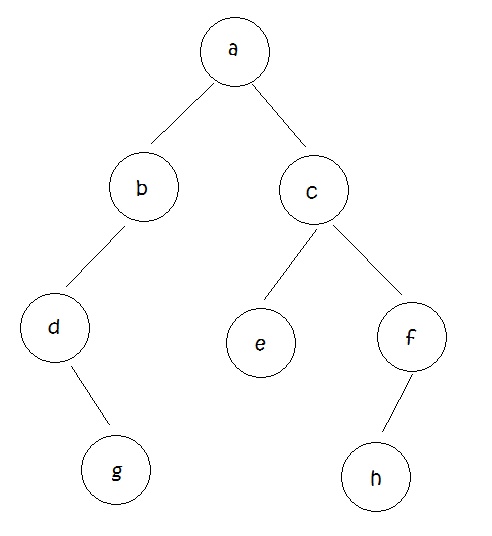

树的转换

树和二叉树之间可以转换，森林于二叉树之间也可以转换，二叉树就是吊

树与二叉树的转换

一般的套路就是画线、抹线、旋转（调整），这个方法就不说了，一搜一大把，利用规律可以不用画线快速写出来，比如下面的一颗简单的树：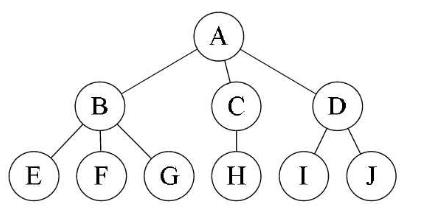

遵循的套路是：如果此节点有孩子，把最左边（或者叫第一个）的孩子挂在左孩子的位置，如果有直接兄弟，就挂在右孩子的位置
按照上面的图画的步骤是：首先 A 是根节点，最左边的孩子是 B ，就把 B 放在 A 的左孩子位置，A 没有兄弟所有右孩子的位置为空；
这样 A 就画完了，继续画 B ，B 的左孩子位置应该是第一个孩子 E , 右孩子应该是 B 的兄弟 C ，依次画下去….最后：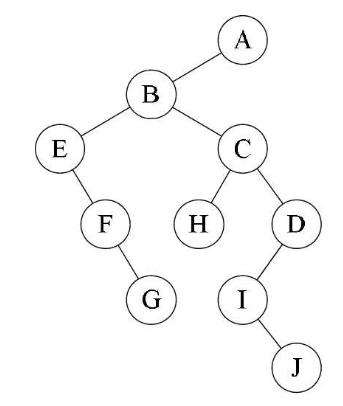

如何把这个二叉树还原成树呢，也很简单，就是逆操作！
套路是：此节点如果有左孩子，就变成其的孩子，它的所有的右分支就是其兄弟
还是上图：A 有左孩子 B ，所以 B 是它（还原成树后的）的孩子，A 没有右孩子，所有没有兄弟，就是所谓的根了！然后再看 B，
B 有左孩子 E ，所以 E 是它的孩子，同时 B 的右分支有 C、D（就是顺着右边那条线下去）；所以 C 和 D 是它的兄弟节点，依次画下去….

由于树根没有兄弟，故树转化为二叉树后，二叉树的根结点的右子树必为空。

森林与二叉树

森林就是由多棵树组成的，所以套路一样，首先把森林里的每棵树按照上面的套路弄成二叉树，树转化为二叉树有个特点就是根节点的右孩子是空的！
所以，找棵树的根作为主根，其他树往主根的右孩子节点上挂就是了，然后最后旋转调整下，其实相当于抓住主根向上拎一下，然后自然就是一个二叉树了！

顺着右孩子数，每一个节点就是一棵树，也能很容易看出这个森林由多少树组成的！
至于拆，也一个样，顺着右孩子的每一个节点拆下来就是一棵树，然后按照上面的套路再还原回去就行了

数据库无限分类设计

在前面说数据库表的设计的时候，有个叫自连接的方案，是给关于分类这种场景用的，使用一张表存，用一个字段指向本表中的父节点的 id ，应该还记得…
这样有个很明显的问题是，当层次很深的时候查询非常慢，因为要递归！

于是，就有好事之人画了这这图：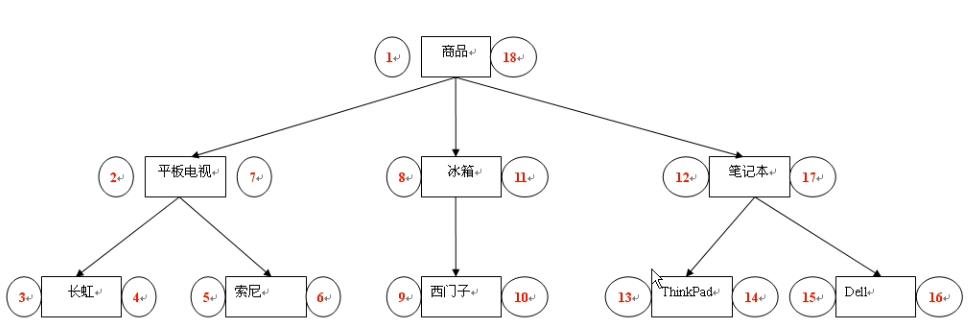

按照这样的结构在数据库存储，很明显这是二叉树，并且还是先序遍历，按照上图设计每一个节点也就是分类、对象的表结构，除了名称和 id 要加一个左值和右值了

通过上面的二叉树的图可以看出有几个特点：

找某个分类下的条目就是左值和右值之间的条目
比如：找笔记本分类下的所有商品就是在 12-17 之间找
层次（深度）就是看属于几个根而决定的，或者说看有几个爸爸
比如：西门子有冰箱和商品两个爸爸，那深度就是3
区分父子节点
爸爸的左值小于孩子的左值；爸爸的右值大于孩子的右值
层次的顺序问题
顺序和左值相关，左值越小的应该排在最前面，当然是对某一分类而言
增加某个节点
只需要把后面的节点的左值右值全部统一加 2 就可以了，用 SQL 语句非常容易就能解决

在设计对象的时候，对象除了表里的“属性”还应有一个层次或者叫深度的属性，这个属性的值可以根据上面的特点算出来，这个很关键，知道层次后才能用代码“画”出这样的树状层次结构

关键在于查询语句的写法了，首先要算出深度，因为父和子都在一张表里存着，哪就把这一张表想象成两张表，一张存父，一张存子，比如下面的 SQL 语句就能查到每个节点的爸爸：

select * from test as parent,test as child where parent.lft < child.lft and parent.rgt > child.rgt;

# ThinkPad  笔记本
# ThinkPad  商品
# ...

也就是说根据某个节点的名称出现多少次就能确定有几个爸爸，也就能确定其的层次，层次就是父节点个数+1；为了方便可以直接把 > 改成 >= 这样就不需要再+1了
想要计算层次（深度），就是计算某个名称（分类）出现了多少次，可以使用 group 进行归组，然后用 count 函数统计下就可以了，完整语句：

1 2	select child.id, child.name,count(child.name) as depth from test as parent,test as child where parent.lft < child.lft and parent.rgt > child.rgt group by(child.name) order by (child.lft);

最后还对左值进行了排序，这样查询出来的数据就是按顺序的：id、名称、深度（层次）了，也就是说每一类的父节点和子节点挨着，封装到对象中进行使用就可以了

用心去去体会！